[译]自上而下的运算符优先解析
介绍
递归下降解析器一直是我感兴趣的,在过去的一年半时间里,我写了几篇关于这个主题的文章。下面是按时间顺序排列的:
第三篇文章介绍了一种将 RD 解析与不同的算法结合起来解析表达式的方法,以达到更好的效果。这种方法在现实世界中实际使用,例如 GCC 和 Parrot 中(来源)。
1973年,Vaughan Pratt 发现了另一种解析算法。称为自上而下运算符优先,它与修改的 RD 解析器有一些共同点,但承诺简化代码,并提供更好的性能。最近它又被 Douglas Crockford 在他的文章中普及,并被他在 JSLint 中用来解析 JavaScript。
我在美丽的代码一书中遇到了 Crockford 的文章,但发现它很难理解。我可以跟着代码走,但很难理解为什么这些会工作。最近,我又对这个话题产生了兴趣,尝试着再读了一次文章,结果又一次陷入了困境。最后,通过阅读 Pratt 的原论文和 Frederick Lundh 的优秀的基于 Python 的作品[1],我理解了这个算法。
所以这篇文章是我通常的尝试,向自己解释这个主题,确保当我在几个月后忘记它的工作原理时,有一个简单的方法来回忆。
基本原理
自上而下的运算符优先解析(以下简称 TDOP)基于几个基本原则:
- 一个“绑定力”机制来处理优先级。
- 一种手段,根据标记相对于其邻居的位置 - 前缀或中缀 - 来实现标记的不同功能。
- 与将语义动作与语法规则(BNF)相关联的传统 RD 相反,TDOP 将其与标记相关联。
绑定力
运算符优先级和结合性是解析技术需要处理的一个基本问题。TDOP 通过给它解析的每个标记分配一个“绑定力”来处理这个问题。
考虑一个子串 AEB,其中 A 取右参数,B 取左参数,E 是表达式。E 是与 A 关联还是与 B 关联?我们为每个运算符定义了一个数字绑定力。具有较高绑定力的运算符“获胜” - 与 E 相关联。让我们检查下这个表达式:
1 + 2 * 4
这里再次列出,标识出了 A,E,B:
1 + 2 * 4
^ ^ ^
A E B
如果想表达乘法比加法有更高优先级的惯例,我们定义 * 的绑定力(bp)为 20,+ 的绑定力为 10(数字是任意的,重要的是 bp(*) > bp(+))。因此,根据上面的定义,2 将与 * 关联在一起,因为它的绑定力高于 + 的绑定力。
前缀和中缀运算符
为了解析传统的中缀符号表达式语言[2],我们需要区分标记的前缀形式和中缀形式。最好的例子是减号运算符(-)。在中缀形式中,它是减法:
a = b - c # a 是 b 减 c
在前缀形式中,它是取反。
a = -b # b 和 a 大小相同但符号相反
为了适应这种差异,TDOP 允许对前缀和中缀语境中的标记进行不同的处理。在 TDOP 术语中,作为前缀标记的处理器称为 nud(代表“空符号”),作为后缀标记的处理器称为 led(代表 "左符号")。
TDOP 算法
这是一个基本的 TDOP 解析器:
def expression(rbp=0):
global token
t = token
token = next()
left = t.nud()
while rbp < token.lbp:
t = token
token = next()
left = t.led(left)
return left
class literal_token(object):
def __init__(self, value):
self.value = int(value)
def nud(self):
return self.value
class operator_add_token(object):
lbp = 10
def led(self, left):
right = expression(10)
return left + right
class operator_mul_token(object):
lbp = 20
def led(self, left):
return left * expression(20)
class end_token(object):
lbp = 0
我们只需要增加一些支持代码,包括一个简单的分词器[3]和解析器驱动:
import re
token_pat = re.compile("\s*(?:(\d+)|(.))")
def tokenize(program):
for number, operator in token_pat.findall(program):
if number:
yield literal_token(number)
elif operator == "+":
yield operator_add_token()
elif operator == "*":
yield operator_mul_token()
else:
raise SyntaxError('unknown operator: %s', operator)
yield end_token()
def parse(program):
global token, next
next = tokenize(program).next
token = next()
return expression()
我们有了完整的解析器和求值器,用于处理涉及加法和乘法的算术表达式。
现在来看看它的实际工作原理。注意,标记类有几个属性(不是所有类都有所有类型的属性)。
- lbp - 运算符的左绑定力。对于中缀运算符,它告诉我们运算符与它左参数的绑定力有多强。
- nud - 前缀处理器。在这个简单的解析器中,它只为字面量(数字)存在。
- led - 中缀处理器。
在这里,启蒙的关键是注意表达式函数是如何工作的,以及运算符处理器如何调用它,传递一个绑定力。
当表达式被调用时,它提供 rbp - 调用它的运算符的右绑定力。它消费标记,直到遇到一个左绑定力等于或低于 rbp 的标记。具体来说,就是在返回调用它的运算符之前,它收集所有绑定在一起的标记。
运算符的处理器调用表达式来处理它们的参数,为它提供它们的绑定力,以确保它从输入中获得恰到好处的标记。
例如,我们来看看这个解析器是如何处理表达式的:
3 + 1 * 2 * 4 + 5
下面是解析器函数在解析这个表达式时的调用追踪:
<<expression with rbp 0>>
<<literal nud = 3>>
<<led of "+">>
<<expression with rbp 10>>
<<literal nud = 1>>
<<led of "*">>
<<expression with rbp 20>>
<<literal nud = 2>>
<<led of "*">>
<<expression with rbp 20>>
<<literal nud = 4>>
<<led of "+">>
<<expression with rbp 10>>
<<literal nud = 5>>
下图显示了不同递归层上对表达式的调用:
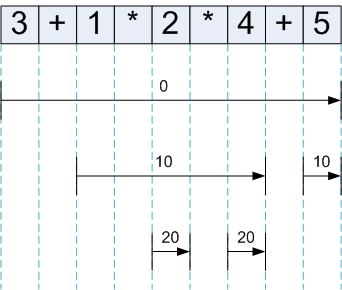
箭头显示了每次执行表达式所依据的标记,上方的数字是这次调用赋给表达式的 rbp。
除了跨越整个输入的初始调用(带有 rbp=0)外,表达式在每个运算符之后被(其 led 处理器)调用,以收集右边的参数。如图所示,绑定力机制确保表达式不会“走得太远” - 只在调用运算符的优先级允许的范围内。理解这个的最好的地方是第一个 + 之后的长箭头,它收集所有的乘法项(由于 * 的优先级较高,它们需要被组合在一起),并在遇到第二个 + 之前返回(当优先级不再高于其 rbp 时)。
另一种看待方式是:在解析器执行的任何一点上,每个优先级都有一个表达式实例在那一刻是活跃的。这个实例等待着更高优先级实例的结果,并一直进行下去,直到需要停止自己,并将结果返回给它的调用者。
如果你理解了这个例子,你就理解了 TDOP 解析。其余所有内容其实都是相同的。
增强解析器
到目前为止,所介绍的解析器是非常初级的,所以我们来增强它,以更加实际。首先,一元运算符呢?
正如在前缀和中缀运算符一节中提到的,TDOP 对两者进行了明确的区分,将其编码在 nud 和 led 方法的差异中。添加减法运算符处理器[4]:
class operator_sub_token(object):
lbp = 10
def nud(self):
return -expression(100)
def led(self, left):
return left - expression(10)
nud 处理减号的一元(前缀)形式,它没有左参数(因为是前缀),对其右参数进行取反。传递到表达式中的绑定能力很高,因为前缀减号有很高的优先级(比乘法高)。led 处理中缀情况类似于 + 和 * 的处理器。
现在我们可以这样处理表达式:
3 - 2 + 4 * -5
并得到一个正确的结果(-19)。
那右关联运算符呢?让我们来实现乘方(使用插入符号 ^)。为了让操作右关联,我们希望解析器将后续的乘方操作符视为第一个操作符的子表达式。我们可以通过在乘方处理器中调用表达式来实现,表达式的 rbp 低于乘方的 lbp。
class operator_pow_token(object):
lbp = 30
def led(self, left):
return left ** expression(30 - 1)
当表达式到了循环中的下一个 ^ 时,会发现仍然 rbp < token.lbp,不会马上返回结果,而是先收集子表达式的值。
那用括号分组呢?由于每个标记都可以在 TDOP 中执行动作,所以可以通过给 ( 标记添加动作来轻松处理。
class operator_lparen_token(object):
lbp = 0
def nud(self):
expr = expression()
match(operator_rparen_token)
return expr
class operator_rparen_token(object):
lbp = 0
其中 match 是通常的 RD 基元:
def match(tok=None):
global token
if tok and tok != type(token):
raise SyntaxError('Expected %s' % tok)
token = next()
请注意, ( 的 lbp=0,意味着它不与左边的任何标记绑定。它被当作一个前缀,它的 nud 在 ( 之后收集一个表达式,直到遇到 ) (它停止表达式解析器,因为它也是 lbp=0)。然后它消耗掉 ) 本身,并返回表达式的结果。[5]
这是完整的解析器代码,处理加、减、乘、除、乘方和括号分组:
import re
token_pat = re.compile("\s*(?:(\d+)|(.))")
def tokenize(program):
for number, operator in token_pat.findall(program):
if number:
yield literal_token(number)
elif operator == "+":
yield operator_add_token()
elif operator == "-":
yield operator_sub_token()
elif operator == "*":
yield operator_mul_token()
elif operator == "/":
yield operator_div_token()
elif operator == "^":
yield operator_pow_token()
elif operator == '(':
yield operator_lparen_token()
elif operator == ')':
yield operator_rparen_token()
else:
raise SyntaxError('unknown operator: %s', operator)
yield end_token()
def match(tok=None):
global token
if tok and tok != type(token):
raise SyntaxError('Expected %s' % tok)
token = next()
def parse(program):
global token, next
next = tokenize(program).next
token = next()
return expression()
def expression(rbp=0):
global token
t = token
token = next()
left = t.nud()
while rbp < token.lbp:
t = token
token = next()
left = t.led(left)
return left
class literal_token(object):
def __init__(self, value):
self.value = int(value)
def nud(self):
return self.value
class operator_add_token(object):
lbp = 10
def nud(self):
return expression(100)
def led(self, left):
right = expression(10)
return left + right
class operator_sub_token(object):
lbp = 10
def nud(self):
return -expression(100)
def led(self, left):
return left - expression(10)
class operator_mul_token(object):
lbp = 20
def led(self, left):
return left * expression(20)
class operator_div_token(object):
lbp = 20
def led(self, left):
return left / expression(20)
class operator_pow_token(object):
lbp = 30
def led(self, left):
return left ** expression(30 - 1)
class operator_lparen_token(object):
lbp = 0
def nud(self):
expr = expression()
match(operator_rparen_token)
return expr
class operator_rparen_token(object):
lbp = 0
class end_token(object):
lbp = 0
示例用法:
>>> parse('3 * (2 + -4) ^ 4')
48
结束语
当人们考虑要实现的解析方法时,通常会在手工编码的 RD 解析器、自动生成的 LL(k) 解析器或者自动生成的 LR 解析器之间进行争论。TDOP 是另一种选择[6]。它是一种独创的、不寻常的解析方法,可以处理复杂的语法(不限于表达式),相对容易编码,而且速度很快。
TDOP 之所以快,是因为它不需要深度递归下降来解析表达式 - 无论语法如何,每个标记只需要几次调用。如果你跟踪我在本文中介绍的示例解析器中的标记动作,你会发现平均而言,对于每个标记,expression 和一个 nud 或 led 方法被调用,仅此而已。Frederik Lundh 在他的文章中对比了 TDOP 和其他几种方法的性能,得到了非常有利的结果。
[1] 这也是本文大部分代码的来源 - 所以版权是 Fredrik Lundh 的。
[2] 如 C、Java、Python。一个没有中缀符号的语言的例子是 Lisp,它的表达式是前缀符号。
[3] 这个分词器只识别数字和单字符运算符。
[4] 请注意,为了让解析器能够实际识别 -,应该在分词函数中添加一个适当的调度器 - 这作为练习留给读者。
[5] 测验:左括号也有 led 处理器有用吗?提示:你如何实现函数调用?
[6] 顺便说一下,我不知道在 LL/LR 量表上该把它归类在哪儿?有什么想法吗?